Classic Camera Collectors Club
Informatieve website van Frank Lakiere


FOTOGRAFIE TECHNISCH BEKEKEN
1. De film
1.1. De opbouw van de lichtgevoelige laag
1.2. Reflecties en halo-verschijnselen

2. Enkele scheikundige grondbegrippen.

3. De ontwikkeling

3.1. De eigenlijke ontwikkeling
3.2. Het stopbad
3.3. Het fixeren
3.4. Het spoelbad

4. Het registratievermogen van de lichtgevoelige laag

4.1. De gevoeligheid van de film
4.2. De registratiemogelijkheden van de film.

5. Lichtgevoeligheid, Sluitertijden en Diafragma

5.1. Licht en afstand
5.2. Licht en lensopening
5.3. Diafragma
5.4. Berekening van de f-waarden reeks
5.5. Gebruik van de f-waarden
5.6. Filmgevoeligheid
5.7. Sluitertijd
5.8. De juiste belichting
5.9. Het Schwarzschild effect en de reciprociteitscorrectie.

6. De technische camera

7. De gaatjescamera

8. Het zonesysteem



Hoofdstuk 1 : De film.


1.1. Opbouw van de lichtgevoelige laag

Het beeld, door de camera gevormd, wordt vastgelegd op de film.
Deze bestaat uit een lichtgevoelige laag - de emulsie - die vast zit op een onderlaag - de drager.
Aan de drager en aan de emulsie worden bepaalde eisen gesteld : ze moeten vooral volledig transparant en stabiel zijn.

Glas is dus een goede drager maar heeft enkele belangrijke nadelen: het is breekbaar en zwaar.
Daarom gebruikt men in de moderne fotografie een plastische onderlaag bv. polyester, celluloidacetaat,...

De samenstelling van de emulsie en de opbouw van de filmlaag hebben een grote invloed op de eigenschappen en kwaliteit van het gevormde beeld.

De emulsielaag (eigenlijk een suspensie) heeft 2 belangrijke komponenten :

1. de zilverhalide (AgX) kristallen (X = bromide of iodide of chloride)
2. gelatine

De emulsielaag is maar enkele honderdsten van een millimeter dik en bevat miljoenen microscopische kristalletjes per vierkante millimeter. Bovenop de emulsie is nog een zeer dunne doorzichtige gelatinelaag aangebracht als beschermingslaag. De emulsielaag wordt op de drager vastgehecht met een adhesielaag en om inwendige reflecties tegen te gaan wordt er ook een antihalolaag aangebracht.


Schematische opbouw van een fotografische filmlaag


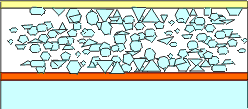
- bovenaan (geel) is er een beschermingslaag tegen mechanische beschadiging
- hieronder heb je de emulsielaag (= AgX kristallen in gelatine). Soms zijn er meerdere emulsielagen, elk met hun specifieke eigenschappen.
- tussen de emulsielagen en de drager is er nog eerst een adhesie- en een antihalolaag (rood)
- de drager (= glas, polyester, celluloidacetaat,...)

De AgX-kristallen zijn lichtgevoelig. Zij leggen het beeld vast.
Dit beeld is eerst nog onzichtbaar en onstabiel; men spreekt van het latent beeld .

Het doel van de fotografische ontwikkeling is:
1. dit latent beeld zichtbaar (ontwikkelbad) maken
2. het zichtbaar beeld permanent (fixeerbad) maken


FOTO'S (vergroting 4000x) van de verschillende filmlagen

Foto 1 : Een hooggevoelige Z/W film


COPYRIGHT: Frank Lakiere

- 1 = oppervlaktebeschermingslaag met UV-filter
- 2 = Hooggevoelige laag met tabulaire kristallen (T-kristallen)
- 3 = laag met kleinere globulaire kristallen
- 4 = antihalo en adhesielaag
- 5 = drager


Foto 2 : een kleurenfilm.


COPYRIGHT: Frank Lakiere

- 1 = oppervlaktebeschermingslaag met UV-filter
- 2 = blauwgevoelige sublaag 1 (grote kristallen => hoge gevoeligheid)
- 3 = blauwgevoelige sublaag 2 (kleine kristallen => lage gevoeligheid)
- 4 = tussenlaag met geelfilter
- 5 = groengevoelige sublaag 1 (grote kristallen => hoge gevoeligheid)
- 6 = tussenlaag oranjefilter
- 7 = groengevoelige sublaag 2 (kleine kristallen => lage gevoeligheid)
- 8 = tussenlaag
- 9 = roodgevoelige sublaag 1 (grote kristallen => hoge gevoeligheid)
- 10 = roodgevoelige sublaag 2 (kleine kristallen => lage gevoeligheid)
- 11 = antihalolaag
- 12 = drager


De gevoeligheid van een film is vooral afhankelijk van de grootte van de AgBr kristallen. Dit is eenvoudig te begrijpen: er is immers een grotere kans dat een groot kristal getroffen wordt door een lichtstraal dan dat dit met een kleiner kristal het geval is. Omdat er meestal gestreefd wordt naar een zo groot mogelijke gevoeligheid zou je denken dat heel grote AgBr kristallen de oplossing zijn. Maar zoals Johan Cruiff ooit zei: "Elk voordeel heb zijn nadeel". Grote AgBr kristallen geven grote gevoeligheid, maar hebben als nadeel dat het bekomen zilverbeeld zeer korrelig is. In een hooggevoelige film wordt hieraan enigszins verholpen door onder de laag met grote AgBr-kristallen een tweede laag aan te brengen met kleine AgBr kristallen, die op de plaatsen waar er veel licht op de film komt ook meebelicht worden en op die plaatsen een bijkomend fijnkorrelig beeld leveren. In de hooggevoelige zwart-wit film komen er verschillende soorten AgBr kristallen voor in 2 lagen: grotere tabulaire kristallen in een bovenste laag en daaronder een tweede laag met kleinere globulaire kristallen.
Waarom die tabulaire (tafelvormig) en globulaire (bolvormig) structuur van de kristallen?
Wanneer AgBr-kristallen gevormd worden dan zijn die min of meer bolvormig. Door de omstandigheden aan te passen kun je kleinere of grotere kristallen maken. Deze bolvormige kristallen worden "globulaire" kristallen genoemd. Alle fotografische films tot 1975 hebben enkel globulaire AgBr kristallen in de emulsie.
Vanaf 1970 stijgt de prijs van zilver op de internationale markten en de filmproducenten onderzoeken hoe ze het verbruik van zilver kunnen beperken. In 1975 is Ciba-Geigy AG de eerste firma die hierover een patent aanvraagt. (Patent US4063951 Manufacture of tabular habit silver halide crystals for photographic emulsions : aanvraag 8 dec 1975 en toegekend op 20 dec 1977). De daaropvolgende 25 jaar wordt er door alle grote filmproducenten (Kodak, Agfa, Ilford en Fuji) heel veel onderzoek gedaan naar deze tabulaire kristallen.

Een tabulair AgBr kristal (afgekort tot T-kristal) is redelijk plat en ziet er uit als een dun zeshoekig plaatje.
In vergelijking met een globulair kristal heeft een T-kristal voor eenzelfde oppervlakte veel minder volume. Een globulair kristal kun je zien als een bol, een T-kristal is dan een schijf uit het midden van de bol. Dit betekent dus dat er veel minder zilver gebruikt wordt bij T-kristallen en hoe groter de kristallen (zoals voor hooggevoelige film) hoe meer zilver er procentueel bespaard wordt. Bij zeer kleine kristallen is het gebruik van de techniek van tabulaire kristallen niet nuttig omdat de besparing aan zilver minimaal is.

Voorbeeld van zilverbesparing bij T-kristallen.
In onderstaande schets stelt de lichtblauwe bol een globulair kristal voor. ,br> Het donkerblauwe gedeelte in elke bol schetst een T-kristal met dezelfde doorsnede.


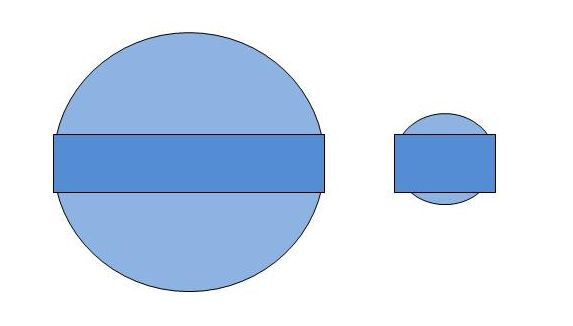
Groot kristal:
Voorbeeld van een T-kristal waarvan de dikte 1/5de is van een globulair kristal met zelfde doorsnede.
Het volume van de bol = 3/4*pi*r*r*r
Het volume van het T-kristal = (r/5)*pi*r*r
Dus is het volume van het T-kristal maar 27 procent van het volume van de bol.
Besparing aan zilver is 73 procent !

Klein kristal:
Hier is de dikte van het T-kristal 2/3de van de diameter van de bol.
Het volume van de bol = 3/4*pi*r*r*r
Het volume van het T-kristal = (2r/3)*pi*r*r
Dus is het volume van het T-kristal hier 80% van het volume van de bol.
Besparing aan zilver is maar 20%.

De productie van T-kristallen is ingewikkelder en duurder dan de productie van 'gewone' AgBr kristallen. Ook is het gieten van de emulsie ingewikkelder, want de T-kristallen moeten in het ideaal geval allemaal plat in de toplaag van de film liggen. Dit is goed te zien in de foto van de hooggevoelige film hierboven. Daarom wordt er in de tweede laag - deze met kleine kristallen- nog steeds gebruik gemaakt van globulaire kristallen.
Een van de bekendste films met T-kristallen is de Kodak T-max.

1.2. Reflecties en halo-verschijnselen.

Het licht dat op de emulsielaag valt wordt door de zilverhalogenidekristallen opgevangen en vormt daar het latent beeld. Maar als er op een plaats heel veel licht valt dan passeert een gedeelte de emulsielaag en dit licht zou door de drager weer teruggekaatst worden in de filmlaag. Dit gereflecteerde licht zou daar de lichtgevoelige kristallen aanvallen en voor een ongewenste zwarting zorgen. Dit noemt men reflectiehalo en het wordt voorkomen door tussen de emulsie en de drager een kleurlaag (antihalo-laag) aan te brengen, die bij het ontwikkelen en fixeren ontkleurt.
Een tweede vorm is de diffusiehalo, die ontstaat doordat de lichtstralen die in de emulsielaag zelf verstrooid worden doordat ze door de kristallen gereflecteerd en verstrooid worden. Dit verschijnsel komt voor bij overbelichting en dus ook bij 'doordrukken' !!



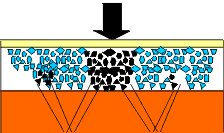
Diffusie- en reflectiehalo




Hoofdstuk 2 : Enkele scheikundige grondbegrippen.


De elementen kunnen in 2 klassen ingedeeld worden : de metalen en de niet-metalen.
Een element dat met zuurstof reageert vormt een oxide.
Sommige oxides zijn water-oplosbaar.
Een oxide van een metaal in water opgelost vormt een base.
Een oxide van een niet-metaal in water opgelost vormt een zuur.
bv.
4 Na + O2 -----> 2 Na2O
Na2O + H2O -----> 2 NaOH
S + O2 -----> SO2
SO2 + H2O -----> H2SO3

Zuren en basen kunnen reageren en vormen dan zouten.
In de fotografische ontwikkeling wordt gebruik gemaakt van zuren, basen en zouten.
De belangrijkste verbinding die in alle processen het hoofdbestanddeel uitmaakt is water.
Water wordt in de ontwikkel-, stop- en fixeerbad gebruikt als reaktiemedium, en dient in de laatste stap om de resten van de chemicaliën uit de emulsie weg te wassen.


Opmerking:
Doordat alle chemische processen bij de ontwikkeling en fixatie in waterig midden gebeuren is het dus zeer belangrijk dat de emulsielaag, waarin zich de zilverhalogenide-kristallen bevinden, gemakkelijk water opslorpt want anders kunnen de reakties niet doorgaan.
Dit is de reden waarom men in de vorige eeuw bij het gebruik van collodium i.p.v. gelatine deze platen nat moest gebruiken. Bij drogen vormt collodium een plastische laag die nog moeilijk water opneemt.




Hoofdstuk 3 : De ontwikkeling



3.1. De eigenlijke ontwikkeling

Na de belichting bevat de emulsie een onzichtbaar en onstabiel beeld.
Door de inwerking van het licht werd in de belichte AgX-kristallen een zeer kleine hoeveelheid metallisch zilver gevormd.
De ontwikkelaar valt nu aan op die Ag-kiemen van de belichte kristallen en vormt het ganse kristal om tot een korrel zwart metallisch zilver. Het latent beeld wordt zichtbaar.


Schematische voorstelling van de ontwikkeling



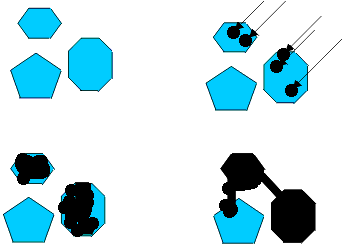
- 1. onbelichte kristallen
- 2. belichting en vorming van zilverkiemen
- 3. ontwikkeling van de kiemen met volledige of gedeeltelijke reductie van het AgX-kristal tot Ag
- 4. bij voortgezette ontwikkeling groeit het zilver tot buiten de grenzen van het kristal en vormt conglomeraten. Dit geeft grove korrels !!!


FOTO'S van zilverbromide kristallen (vergroting 10.000 x)

Onbelichte zilverbromide kristallen.

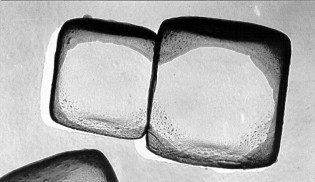
COPYRIGHT: Frank Lakiere


Belichte zilverbromide kristallen, waarbij de zilverkiemen - na een korte zachte ontwikkeling - duidelijk te zien zijn.


COPYRIGHT: Frank Lakiere


De ontwikkelaar is meestal een organische stof bv. hydroquinone.
Maar een oplossing van de ontwikkelaar (developing agent) en water alléén werkt niet goed.
Een ontwikkelaar bevat nog enkele produkten, namelijk:

- een activator
- een bewaarmiddel
- een remstof


a. Omdat een ontwikkelaar maar goed werkt bij een pH>7 wordt er een base aan toegevoegd bv.Na2CO3, NaOH. Naarmate de pH hoger is werkt de ontwikkelaar sneller. Omdat de base nodig is om de ontwikkelaar aktief te maken, noemt men deze de activator.

b. Een ontwikkelaar die aan de lucht blootgesteld is, wordt na verloop van tijd bruin. Dit komt doordat er oxidatie optreedt. Dit wordt tegengegaan door de ontwikkelaar zoveel mogelijk af te schermen van de luchtzuurstof en door er een anti-oxidans aan toe te voegen, meestal Na-sulfiet. Dit is dus het bewaarmiddel .

c. Een ontwikkelaar valt eerst en vooral aan op de metallische zilverkiem van een belicht AgX-kristal, maar hij gaat daarna ook de niet-belichte kristallen ontwikkelen. Als in een emulsie ook niet-belichte kristallen ontwikkeld worden levert dit een mistig beeld op. Men spreekt dan van fog.
Daarom wordt er een remstof (restrainer) aan de ontwikkelaar toegevoegd (meestal KBr).


3.2. Het stopbad

Hoe langer een fotografische emulsie in het ontwikkelbad blijft, hoe donkerder het resulterend beeld zal zijn, en hoe meer kans er bestaat op vorming van fog.
Als het beeld juist genoeg ontwikkeld is, wordt het ontwikkelproces gestopt door gebruik te maken van een zuur stopbad . Doordat de ontwikkelaar enkel werkt bij pH>7 (=base) wordt de ontwikkeling direkt gestopt door de emulsie in een oplossing van pH<7 (=zuur) te brengen.
Meestal gebruikt men als stopbad een oplossing van azijnzuur in water, maar citroenzuur wordt ook gebruikt.


3.3. Het fixeren

Na de ontwikkeling is het beeld wel zichtbaar, maar nog niet houdbaar.
Immers de belichte AgX-kristallen zijn omgezet tot metallisch zilver en de ontwikkeling werd op een gunstig moment gestopt in een stopbad, maar de emulsie bevat nog alle niet-belichte AgX-kristallen. Deze zijn nog steeds lichtgevoelig en als ze in de emulsie blijven zullen ze mettertijd steeds maar donkerder worden en zo wordt het beeld onherkenbaar.
Het fixeerbad verwijdert de onbelichte AgX-kristallen uit de emulsie en maakt zo het fotografisch beeld permanent .
Het belangrijkste produkt in een fixeermiddel is natriumthiosulfaat.
Dit werd vroeger ook wel natriumhyposulfaat genoemd, en vandaar wordt het fixeerbad soms nog wel eens gewoon "hypo" genoemd.
Teneinde het fixeren goed te laten verlopen zijn er ook hier nog enkele hulpprodukten bij nodig.
a. Het stopbad heeft de ontwikkeling wel gestopt maar misschien zijn er nog resten van de ontwikkelaar overgebleven. Deze worden geneutraliseerd door aan de fixeeroplossing zuur toe te voegen. Zo te zien is het stopbad dus niet alleen nuttig omdat het de ontwikkeling stopt, maar het stopbad verlengt ook de levensduur van het fixeerbad.
b. Uit thiosulfaat wordt gemakkelijk colloïdaal zwavel gevormd. Aan de fixeer wordt daarom als bewaarmiddel natriumsulfiet toegevoegd.
Natriumsulfiet werkt hier niet als antioxidans zoals bij de ontwikkelaar, maar het gevormde zwavel reageert met sulfiet en vormt opnieuw thiosulfaat.
c. De gelatine in de emulsie wordt zacht in het ontwikkelbad. Teneinde een te grote opzwelling tijdens het wassen tegen te gaan wordt in het fixeerbad een verharder toegevoegd.
d. De verharder beschermt de emulsielaag, maar hij werkt enkel bij een pH van ±4. Teneinde de pH van het fixeerbad ongeveer konstant te houden wordt een buffer toegevoegd. Dit is meestal borax.


3.4. Het spoelbad

Het laatste wat nog dient te gebeuren is spoelen, om de resten van het fixeerbad uit de emulsie te verwijderen.
Fixeerresten in de emulsie geven na enige tijd aanleiding tot verkleuringen en vlekken. Het spoelen dient dus rigoureus te gebeuren om het fotografisch beeld onveranderd te kunnen behouden.






Hoofdstuk 4 : Het registratievermogen van de lichtgevoelige laag


4.1. De gevoeligheid van de film

Deze wordt vooral bepaald door de grootte van de zilverhalogenide kristallen in de emulsie.
Een groot kristal heeft meer kans om door een lichtstraal getroffen te worden dan een klein kristal.
Dus: hoe gevoeliger de film hoe groter de korrel zal zijn.
Een grovere korrel kan ook het gevolg zijn van de diffusiehalo die ontstaat bij overbelichting van het negatief en bij doordrukken op fotopapier (zie hoger).
Men kan een kleinere korrel krijgen door de keuze van de ontwikkelaar en ook door de ontwikkelaar binnen zekere grenzen verdund te gebruiken. Ook de beweging tijdens het ontwikkelen speelt een rol.
Teneinde het ontstaan van grove korrels door overontwikkeling van de kristallen tegen te gaan worden in de emulsie stoffen ingebracht die de ontwikkeling enigszins afremmen.

Interessant is ook de evolutie van de filmgevoeligheid in de tijd.

Vanaf de tijd van Nièpce en Daguerre tot nu is er ononderbroken gezocht naar verhoogde filmgevoeligheid, de zogenaamde snellere emulsies. Een kort overzicht van deze stijging is dan ook zeer interessant:

1827 : Nièpces asfaltprocédé : belichtingstijd : 6-8 uur
1839 : Daguerreotypie met zilverjodide : 30 minuten
1841 : Talbotypie met galluszuur ontwikkelaar : 3 minuten
1851 : Nat collodiumprocedee : 10 seconden
1864 : Collodium zilverbromide emulsie : 15 seconden
1878 : Gelatine zilverbromide emulsie : 1 tot 1/200 seconde
1900 : Gelatine zilverbromide wordt verbeterd tot belichtingstijd van 1/1000 seconde


Ook wat betreft de spectrale gevoeligheid werd vooruitgang geboekt:
De Daguerreotype platen waren enkel gevoelig voor UV, blauw en een beperkt deel van het visuele spectrum.
Het gebruik van "sensitizers" maakte dat de gelatine-emulsies voor een breder spectrum gevoelig waren. De orthochromatische film was nog redelijk ongevoelig voor rood licht, maar de panchromatische film bestrijkt het gehele visuele spectrum en het nabije UV.
Door gebruik te maken van kwartslenzen is het ook mogelijk om het gebied tot het verre UV uit te breiden en met de gepaste sensitizers kan ook het infra-rood gebied bestreken worden.


4.2. De registratiemogelijkheden van de film.

De zilverhalogenide kristallen zijn eigenlijk maar gevoelig voor welbepaalde kleuren. Omdat zilverhalogenide kristallen een lichtgele kleur hebben absorberen ze gemakkelijk blauw en violet en natuurlijk in sterke mate ultra-violet, maar ze reflecteren de andere kleuren.
Geel, groen en rood zijn dus nauwelijks in staat om een kristal binnen te dringen om zo de energie te leveren die een zilverkiem doet ontstaan.
Zo kan men natuurlijk nooit een goede weergave van de werkelijkheid bekomen. Daarom voegt men aan de emulsie stoffen toe die deze kleuren wel absorberen en zo de energie aan de zilverhalogenide kristallen doorgeven. Met een geschikte rode kleurstof maakt men de emulsie gevoelig voor groen licht, met een groene kleurstof voor rood licht.
Oudere films waren vooral geel- en groengevoelig en weinig roodgevoelig. Dit noemt men orthochromatische film. Deze films kunnen in een doka bij donkerrood licht behandeld worden en ze worden nog veel gebruikt voor technische toepassingen.
De gewone moderne films die voor alle kleuren gevoelig zijn noemt men panchromatische films.
Ons oog heeft de mogelijkheid om een veel groter gebied van contrasten te registreren dan de film. Het gebied waarin een film nog juist detail geeft in diep zwart en in fel licht is minstens 100 x beperkter dan ons oog.
De registratie-omvang van een film bedraagt theoretisch 7 diafragmastops. Maar dit kunnen we in de praktijk terugbrengen tot 5 diafragmastops. Met 3 stops over- en 2 stops onderbelicht hebben we nog steeds detail in de donkerste en helderste partijen. Hier is het mogelijk om door tegenhouden en doordrukken dit detail in de foto naar voor te halen. Buiten deze grenzen is er enkel zwart of wit: daar heeft tegenhouden of doordrukken geen zin.
Bijvoorbeeld:
We meten met een lichtmeter de juiste belichting bij een opname en we vinden dat voor de juiste weergave van middengrijs een diafragma f:8 en een tijd t:125 nodig is.
Hieronder geven we de schaal van de diafragmawaarden weer en daaronder het resultaat
- voor de film
- voor de foto
- en wat te doen indien het resultaat niet goed is.


1.4 ..... 2 ..... 2.8 ..... 4 ..... 5.6 ..... ***8*** ..... 11 ..... 16 ..... 22 ..... 32 ..... 45

-------------------------------------------- GOED ------------------------------------------------
OVERBELICHTING .................................................................. ONDERBELICHTING
Negatief is te donker .............................................................. Negatief is te licht
Foto is te licht ........................................................................... Foto is te donker
bij afdrukken : doordrukken ................................... bij afdrukken : tegenhouden




Hoofdstuk 5 : Gevoeligheid, diafragma en sluitertijd


5.1. Licht en Afstand

De hoeveelheid licht die per oppervlakte-eenheid een voorwerp bereikt vermindert ongelooflijk snel naarmate de afstand vergroot.
Bekijken we een lichtbron die door een gaatje in een scherm een lichtbundel geeft met een lichthoeveelheid L.

Op 1 meter afstand is de bundel gespreid over een oppervlakte met straal r (dus met diameter d = 2r) en de belichte oppervlakte is π r2.

Op 2 meter is de straal van de belichte oppervlakte 2x zo groot en de oppervlakte is dus Π (2r)2 = 4Π r2
Op 3 meter is de straal 3x zo groot en de oppervlakte dus Π (3r)2 = 9Π r2


Zo zien we dat dezelfde hoeveelheid licht L op verschillende afstanden een oppervlak belicht dat evenredig is met het kwadraat van die afstand.

De lichthoeveelheid per oppervlakte-eenheid zal dus afnemen evenredig met het kwadraat van de afstand.


5.2. Licht en Lensopening

Als we een lichtbron door een rond gaatje laten schijnen, dan komt er meer licht door naarmate het gaatje groter wordt. De doorgelaten lichthoeveelheid is evenredig met de oppervlakte van de opening.
Bij een ronde opening is de oppervlakte van de opening Π x r2.
Bijgevolg is de doorgelaten lichthoeveelheid evenredig met het kwadraat van de straal van de opening.
Opm: vermits de straal de halve diameter is kan je dit ook uitdrukken als :
de doorgelaten lichthoeveelheid is evenredig met het kwadraat van de diameter.


5.3. Het diafragma

De diafragma-opening wordt weergegeven door de f-waarde.
De f-waarde is de breuk die de verhouding van de diameter van de lensopening (d) tot de brandpuntsafstand of focale lengte (F) van de lens weergeeft.

Bijv: een lens met brandpuntsafstand 50 mm ;
bij een lensopening met diameter 25 mm is de f-waarde 25/50 =1/2
bij een lensopening met diameter 12,5 mm is de f-waarde 12,5/50 = 1/4.
Men noteert echter alleen de deler van deze breuk dus f/2 en f/4.

Bijgevolg correspondeert een hogere f-waarde met een kleinere lensopening.


5.4. Berekening van de f-waarden reeks

Bij een lens is de hoeveelheid doorkomend licht L evenredig met het kwadraat van de diameter van de lensopeningen dus L = k.d2 (k = evenredigheidsfactor).
Bij een lens met brandpuntsafstand F = 100mm
en diameter lensopening d =100mm geeft dit:
Bij volledige opening: d = 100 mm en dus L = k.100.100 = k.10000
En f = d/F = 100/100 dus deze lensopening is f/1

Een halvering van het licht geeft L= (k.10000):2 = k.5000
Dit correspondeert met diameter van lensopening
d = vierkantswortel van 5000 of d =70,71 mm
en f-waarde = d/F = 70,71/100 = 1/1,41 of dus een lensopening van f/1,4

Nog eens halveren levert d = vierkantswortel van 2500, dus d = 50 mm
en f-waarde = 50/100 = 1/2 en dus een lensopening f/2

Volgende halvering levert d = vierkantswortel van 1250, dus d =35,35 mm
en f-waarde = 35,35/100 = 1/2,82 of dus f/2,8

En zo verder: d = vierkantswortel van 625 = 25 mm
f = 25/100 = 1/4 en dus lensopening f/4

d = vierkantswortel van 312 = 17,68 mm
f = 17,68/100 = 1/5,65 of dus f/5,6

d = vierkantswortel van 156 = 12,5 mm
f = 12,5/100 = 1/8 of dus f/8

d = vierkantswortel van 78 = 8,839 mm
f = 8,839/100 = 1/11,3 en dit geeft f/11

d = vierkantswortel van 39 = 6,245 mm
f = 6,245/100 = 1/16,0 of lensopening f/16

enz... vervolgens f/16 - f/22 - f/32 - f/45 - f/64 - f/90 - f/128 - f/180 - ...

Het is dus zo dat
ieder volgend f-nummer = het voorgaande f-nummer x de vierkantswortel van 2 (= 1,414)
Dat geeft de reeks f-waarden waarbij telkens een halvering van de lichthoeveelheid optreedt:
1 : 1,4 : 2 : 2,8 : 4 : 5,6 : 8 : 11 : 16 : 22 : 32 : 45 : 64 : 90 : 128 : 180 : 256 enz.
Opmerkingen: Bovenstaande reeks is de 'moderne' F-reeks, zoals ze meestal op de lenzen van reflextoestellen aangebracht is.
De volledige reeks voor professionele cameras met 1/3de diafragmastops ziet eruit als volgt:

1 - 1.12 - 1.26 - 1.4 - 1.6 - 1.8 - 2 - 2.2 - 2.5 - 2.8 - 3.2 - 3.6 - 4 - 4.5 - 5 - 5.6 - 6.3 - 7.1 - 8 - 9 - 10 - 11 - 12.7 - 14 - 16 - 18 - 20 - 22 - ...

Voor deze 1/3de stop reeks is ieder volgend f-nummer = het voorgaande f-nummer x 1.1225
(dit is de zesde wortel van 2 )

Bij oudere lenzen komt soms de reeks voor beginnend met f/4.5 of f/6.3 en voor de volle stop f-reeks krijg je dus:
4.5 - 6.3 - 9 - 12.7 - 18 - 25 - 36 - 50 - ...

Heel grote f-waarden komen voor bij de gaatjescamera. Als we bij zulke camera een lensopening hebben van 0.2 mm en de afstand van de lens tot de film is 7 cm (70 mm) dan is de f-waarde 0.2/70 = 1/350 en dus f/350.


5.5. Gebruik van de f-waarden

Een voordeel van het gebruik van de f-waarde is dat bij verschillende objektieven dezelfde f-waarde aanleiding geeft tot dezelfde lichthoeveelheid door de lens.
Bijv: lens van 50 mm met f/8 heeft lensopening met diameter d
en een lens van 135 mm en f/8 heeft lensopening met diameter D
f-waarde = diameter/brandpuntsafstand of dus
voor 50 mm lens 1/8 = d/50 en dus is d = 50/8 = 6,25 mm
voor 100 mm lens 1/8 = D/100 en dus is D = 100/8 = 12,5 cm
Het opvallend licht L is evenredig met het kwadraat van de diameter van de opening en omgekeerd evenredig met het kwadraat van de afstand
dus voor 50 mm lens L = k. 6,25. 6.25/ 50. 50 = k. (6,25/50)2 = k.(1/8)2
en voor de 100 mm lens L = k.12,5.12,5/100.100 = k(12,5/100)2 = k(1/8)2

Bijgevolg is de f-waarde een maat voor de hoeveelheid licht die door de lens op de film valt en dit onafhankelijk van de brandpuntsafstand van de lens.




5.6. Filmgevoeligheid

Niet alle lichtgevoelige emulsies zijn even gevoelig.
Er zijn films met lage gevoeligheid, die dus meer licht nodig hebben dan de films met hoge gevoeligheid, die het met minder licht kunnen stellen.

Om films onderling te kunnen vergelijken zijn er heel wat verschillende gevoeligheidsschalen opgesteld: Kodak Speeds, Weston, Scheiner, Ilford, ... (vergelijkbaar met de temperatuurmeting in °Celsius, °Fahrenheit, maar ook °Kelvin en vroeger °Réaumur).
Ilford gebruikte als enige letters om de filmgevoeligheid aan te geven. Zo was een "A" gelijk aan 4 ASA, "C" = 16 ASA, "E" = 64 ASA, "G"= 256 ASA en "H" = 512 ASA.
De engelse Scheiner schaal is (zoals de DIN schaal) exponentieel.
In de Sovjetunie werd de GOST schaal gebruikt tot 1997. Deze schaal komt in grote lijnen overeen met de ISO schaal.
Het ASA systeem uit 1958 is gebaseerd op het werk van L.A. Jones van de Kodak Research Laboratories. Zijn idee was om een waarde te vinden voor een minimale belichting waarbij nog een uitstekende afdruk kan bekomen worden. De methode van Jones is zeer omslachtig en werd oorspronkelijk alleen gebruikt door Kodak vanaf 1940. Deze waarden werden 'Kodak Speeds' genoemd.
ASA neemt deze methode over maar voert een veiligheidsfactor in van één f-stop.
In 1958 werd deze methode aangepast. De methode is nu - zoals de Duitse DIN methode - gebaseerd op het vinden van een minimale densiteit voor een bepaald gemiddeld contrast.
Terzelfdertijd werden nog enkele aanpassingen doorgevoerd zodat dezelfde film die in 1940 een Kodak Speed van 100 heeft, in 1958 een ASA waarde krijgt van 25.


ISO 6:1993 methode om filmgevoeligheid te bepalen van een zwart-wit film.



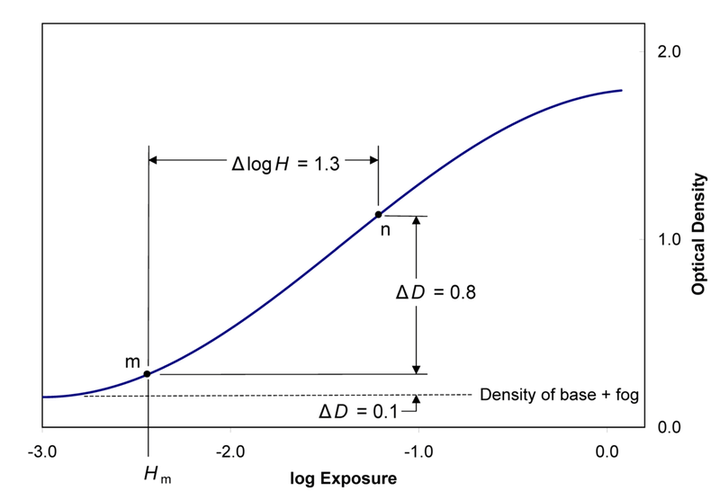
De filmgevoeligheid wordt gevonden door een curve te tekenen van de optische densiteit tegenover de logaritme van de belichting. Deze curve is gekend onder de naam Hurter-Drifield curve (of ook wel D-log H curve).
Deze curve bestaat gewoonlijk uit 5 delen : de basis, de voet, het lineair gebied, de schouder en het overbelicht gebeid.
Voor zwart-wit films ligt het snelheidspunt m op de curve waar de densiteit de waarde van de basis + 0.1 overschrijdt. Dit is wannneer het negatief zo ontwikkeld is dat het punt n waar de log van de belichting 1.3 eenheden groter is dan de belichting op punt m een densiteit heeft die 0.8 keer groter is dan op punt m.
De belichting Hm (in lux-s) is deze voor punt m wannneer aan de specifieke contrast voorwaarde voldaan is.
De ISO waarde voor deze film is dan S = 0.8/Hm

Voor kleurfilm is de bepaling van de ISO waarde gelijkaardig, maar dan wordt er wel rekening gehouden met de curven voor blauw, groen en rood.


Er zijn lange tijd 2 systemen blijven bestaan: DIN (Deutsche Industrie Norm) en ASA (American Standards Association).
De DIN schaal is exponentieel en wordt uitgedrukt in graden. Een verschil van 3 graden geeft een verdubbeling aan van de gevoeligheid. Een film van 24° DIN is dubbel zo gevoelig als een 21° DIN film.
Bij de ASA schaal is de gevoeligheid evenredig met het getal: een film die tweemaal gevoeliger is heeft een tweemaal zo groot ASA-getal.
Uiteindelijk heeft de International Standards Organisation een combinatie van deze twee systemen als ISO-standaard voorgesteld.

De ISO-waarde bestaat dus uit 2 getallen:
eerst de ASA-waarde, gevolgd door de DIN-waarde (bijv. ISO 400/27°).

Lijst van de meest voorkomende waarden:

ASA = 25 ; DIN = 15 ; ISO = 25/15° ; bijv. Technical Pan, Agfa Ortho
ASA = 50 ; DIN = 18 ; ISO = 50/18°
ASA = 100 ; DIN = 21 ; ISO = 100/21° ; bijv. T-Max 100, Agfapan 100
ASA = 200 ; DIN = 24 ; ISO = 200/24° ; bijv. Kodak Gold 200
ASA = 400 ; DIN = 27 ; ISO = 400/27° ; bijv. T-Max 400
ASA = 800 ; DIN = 30 ; ISO = 800/30°
ASA = 1600 ;DIN = 33 ; ISO = 1600/33°

Maar er zijn ook bekende tussenliggende waarden:
ASA = 64 ; DIN = 19 :ISO = 64/19° ; bijv. Ektachrome 64
ASA = 125 ; DIN = 22 ; ISO = 125/22° ; bijv. Ilford FP4, Kodak Plus-X
ASA = 320 ; DIN = 26 ; ISO = 320/26° ; bijv. Tri-X Prof
ASA = 1000 ; DIN = 31 ; ISO = 1000/31° ; bijv. Ektar 1000

Opmerking: de gevoeligheid van Z/W fotopapier is ongeveer 5 ASA.



5.7. Sluitertijden

De sluitertijd wordt weergegegeven in seconden of fracties van een seconde (bv. 1/30 sec; 1/1000 sec) en geeft de totale tijd weer dat de film belicht wordt. Deze wordt bepaald door de sluiter van de camera gedurende een welbepaalde tijd te openen.
De hoeveelheid licht die op de film valt is evenredig met de belichtingstijd.
Als we de sluitertijd halveren, dan halveren we ook de hoeveelheid licht die op de film valt.
Op de moderne toestellen komt volgende reeks sluitertijden voor (in seconden)
1 : 1/2 : 1/4 : 1/8 : 1/15 :1/30 : 1/60 : 1/125 : 1/250 : 1/500 : 1/1000 : 1/2000
Zoals bij de diafragmawaarde f wordt ook hier niet de breuk maar enkel de noemer van de breuk vermeld.

De reeks van de belichtingstijden is dus:
1 : 2 : 4 : 8 : 15 : 30 : 60 : 125 : 250 : 500 : 1000 : 2000


5.8. De juiste belichting

Om de juiste belichting te bekomen moet een evenwicht bereikt worden tussen het licht dat door de lens op de film valt en de gevoeligheid van de film.
Het licht dat door de lens op de film wordt bepaald door diafragma en belichtingstijd. Samen met de filmgevoeligheid zijn er dus 3 parameters.

Bijvoorbeeld: elk van de volgende instellingen geeft dezelfde belichting

instelling A: film 50 ISO; f/11; 1/60 sec
instelling B: film 50 ISO; f/16; 1/30 sec
instelling C: film 100 ISO; f/16; 1/60 sec
instelling D: film 400 ISO; f/11; 1/500 sec

Zo moet je dus altijd kiezen voor een meer of minder gevoelige film, een groter of kleiner diafragma en een kortere of langere belichtingstijd. De uiteindelijke keuze is meestal een compromis want een grotere lensopening geeft minder scherptediepte, maar kiezen voor een hooggevoelige film geeft dan weer een grovere korrel (= slechtere filmresolutie).
Bij heel kleine lensopeningen treedt diffractie op aan de randen van het diafragma wat ook de beeldkwaliteit beïnvloedt.
Tijden langer dan 1/60 sec geven gemakkelijk bewegingsonscherpte, dus daarbij dien je een statief te gebruiken. Maar bij tijden langer dan 2 sec moet je daarbij ook nog rekening houden met het Schwarzschild effect.

Maar hoe bepaal je dan de juiste belichting?
De meeste moderne kleinbeeldcameras hebben een ingebouwde belichtingsmeter. Bij een diafragma-voorkeuze systeem kies je zelf het diafragma en het camerasysteem bepaalt welke tijd er moet belicht worden.
Bij een sluiter-voorkeuze systeem kies je zelf de sluitersnelheid en de camera past zijn diafragma aan.
Meestal is er ook een AUTO methode voorzien. Hierbij kiest de camera zowel de tijd als het diafragma en stelt zelf ook scherp (autofocus). De fotograaf moet dus alleen maar het beeld samenstellen en op de ontspanknop drukken.

Bij gebruik van oudere toestellen zonder lichtmeter kun je de zogenaamde "sunny 16" regel toepassen.
Dit betekent dat je in zonnig weer en met een ISO 100 film en met 1/100 sec sluitersnelheid een goede belichting krijgt bij diafragma f/16.

5.9. Het Schwarzschild effect en de reciprociteitscorrectie.

In fotografie verwijst de term 'recoprociteit' naar de relatie waarbij de totale lichtenergie het effect van het licht op de film bepaalt. Deze lichtenergie is afhankelijk van de belichtingstijd en van de lichtintensiteit. Deze 2 parameters worden bij een fototestel bepaald door het diafragma en de sluiter.
Wanneer je nu onder normale omstandigheden het diafragma meer sluit en bvb. 2x minder licht doorlaat, dan kan je dit compenseren door de sluitersnelheid met dezelfde factor aan te passen. Er is dus onder normale omstandigheden voor een bepaald fotografisch resultaat een reciprociteit tussen de disfragma-opening en de sluitersnelheid.
bvb. Je krijgt een goede belichting van een bepaalde scène met een diafragma f/8 en sluitersnelheid 1/250 sec.
Verandering van het diafragma naar f/11 geeft 2x minder licht en dat compenseer je door de sluitersnelheid van 1/250 sec naar 1/125 sec aan te passen.
Bij reciprociteit geldt dus dat diafragma en sluitersnelheid gekoppeld zijn, waarbij bij verandering van diafragma met een faktor k, de sluitersnelheid moet aangepast worden met een faktor 1/k.
Het resultaat op de film zou dan hetzelfde blijven.

Bij heel lage lichtintensiteit reageert de film minder goed op belichting. Men kan licht zien als een stroom van aparte fotonen en de fotografische emulsie als een laag aparte lichtgevoelige korrels (meestal zilverhalogenide). Deze korrels vormen een latent beeld wanneer ze getroffen worden door een lichtstraal. Maar om deze reactie in gang te zetten zijn er meerdere fotonen nodig per korrel. Wanneer het oppervlak van een zilverhalogenide kristal een groepje van 4 of meer zilveratomen heeft die door fotonen zijn gereduceerd tot zilver, dan is het mogelijk voor een ontwikkelaar om dit kristal te ontwikkelen. Hiervoor zijn enkele tientallen fotonen nodig.
Bij heel lage lichtintensiteit, en dus met heel weinig fotonen per tijdseenheid, dan komen de fotonen met een groter interval aan op het zilverkristal. Wanneer de 4 fotonen die nodig zijn om het kristal 'ontwikkelbaar' te maken over een te lange periode verspreid aankomen, dan is de gedeeltelijke reductie van het kristal niet stabiel genoeg om te overleven totdat er genoeg fotonen aangekomen zijn zodat een stabiel latent beeld gevormd wordt.
Dit maakt dat de reciprociteitsregel niet meer geldt en dat een langere belichtingstijd nodig is.

Wanneer de lichtintensiteit zo laag wordt dat het reciprociteitsbereik overschreden wordt, dan moet de belichtingstijd gecorrigeerd worden met een reciprociteitsfactor.
Dit noemt men het Schwarzschild effect of de 'reciprocity failure' en het wordt meestal duidelijk waargenomen vanaf een belichtingstijd van 1 seconde. Elke film heeft zijn eigen respons bij lage lichtintensiteit en het is dus nodig om per film te testen wat de juiste reciprociteitsfactoren zijn.

Opmerking : ENKELE OPMERKINGEN

1.
Zeer lage lichtintensiteit komt ook voor bij zeer korte belichtingstijden. Dit is meestal geen probleem voor de gewone fotograaf, maar het komt voor bij wetenschappelijke of technische fotografie waar soms belichtingstijden van minder dan 1 milliseconde gebruikt worden. 2.
Bij de gewone kleinbeeldcamera wordt meestal per volledige of halve diafragmastop gewerkt.
Bij een studiocamera wordt meestal gerekend per 1/3de diafragmastop.
Het is dus niet toevallig dat in de DIN-reeks een verandering van 1° overeenkomt met een verandering van 1/3de diafragmastop.

3.
Bij een elektronische camera laat de elektrische bediening van het diafragma toe om de schaal van de diafragmastops in kleinere tussenstappen op te delen dan bij de mechanische camera.

4.
Bij flitsmeters wordt de lichtmeting zelfs tot op één tiende van een diafragmastop weergegeven. Voor studiowerk is het soms nodig om grote oppervlakken zeer gelijkmatig uit te lichten en hierbij is digitale lichtmeting tot 1/10de stop een belangrijk hulpmiddel.
Bij het gebruik van diafilm is een zeer juiste belichting noodzakelijk, want er kan na de ontwikkeling niet meer gecorrigeerd worden.

5.
Bij het spreken over 'een stop meer' of 'een stop minder' wordt steeds uitgegaan van het standpunt van de film: 'een stop meer' betekent dus meer licht geven en dit is een grotere opening (= kleinere f-waarde).





Hoofdstuk 6 : De technische camera


Hierna volgt een summiere beschrijving van de technische camera.
De monorail technische camera is eigenlijk theoretisch een zeer eenvoudige camera. Hij bestaat uit een lenshouder met lens vooraan, een matglas/negatiefhouder achteraan, een uitschuifbare balg daartussen en een rail waarop het geheel gemonteerd is.
Hierna een schema van een monorail technische camera, een TOYO-VIEW CX45.


  1. = de achterwand met matglas en verwisselbare negatiefhouders. De achterwand is verstelbaar (op, neer, links, rechts en kantelen)
  2. = voorkant met de lenshouder. Deze kan ook in alle richtingen versteld worden.
  3. = de bedieningsknoppen voor verstelling van voor- en achterkant
  4. = de monorail
  5. = de uittrekbare balg
  6. = systeem om camera op statief vast te maken
  7. = schuifknoppen voor het focuseren
  8. = ingebouwd waterpas
  9. = verwisselbare lensplaat

Naast de monorail, zijn er ook technische cameras die voorgemonteerd zijn. Ze kunnen dan open- en dichtklappen en zijn dus gemakkelijker op te stellen. Een van de mooiste hedendaagse technische cameras van deze soort wordt gemaakt door WISNER (USA)



De Wisner Technical Field camera


Deze camera wordt gemaakt in verschillende groottes, namelijk voor 4x5 inch, 5x7 inch en zelfs 8x10 inch negatieven (of dus ongeveer: 10x13, 13x18 en 20x25 cm)

Meer info over grootformaat cameras vind je ondermeer op volgende site: http://www.camerareview.com





Hoofdstuk 7 : Fotograferen met een GAATJESCAMERA


Goed fotograferen met een pinhole camera is wel iets gecompliceerder dan een gaatje maken in een zwarte doos, maar niet veel meer.
Je moet natuurlijk wel de basiskennis hebben van zwart-wit ontwikkeling.

Eerst wat over de 'lens' van onze gaatjescamera.
 Een pinhole werkt op een heel andere manier dan een lens. Een lens bundelt het licht dat erop invalt en buigt de stralen af zodat ze samenkomen in het brandpunt of de focus. Men zegt dat de lens de lichtstralen focuseert.
Een pinhole is meer een filter. Het gaatje laat gewoon een zeer fijne stralenbundel door. In een ideale situatie zou het gaatje zo smal zijn dat er per punt van het object maar een enkele lichtstraal doorgelaten wordt. In de praktijk kan dit niet, omdat licht een golfkarakter heeft en er bijgevolg bij de doorgang van licht door een zeer smalle opening afbuiging of diffractie optreedt. Deze afbuiging heeft onscherpte tot gevolg.
In de praktijk is een pinhole zo groot dat er een stralenbundel doorgelaten wordt en die geeft voor ieder punt van het gefotogreerde object op het filmvlak een rond vlekje i.p.v. een enkel punt. De grootte van de cirkel van de lichtvlek bepaalt hoe scherp het beeld is.

Vergelijking pinhole vs. lens

Diafragma of f-waarde van een gaatjescamera
De afstand van het gaatje (= de lens) tot het negatief is de brandpuntsafstand (s). Als je diameter van het gaatje kent dan is het diafragma f= s/D

De beeldgrootte
Als
i = de grootte van het beeld op de film
j = de groote van het echte object
s = de brandpuntsafstand van de gaatjescamera (d.i. afstand gaatje tot film)
a = afstand van camera tot object
dan is i/s = j/a
en dus is de beeldgrootte i = s x j/a
Dus hoe groter de brandpuntsafstand van de camera, hoe groter het negatiefbeeld.



De optimale grootte van het gaatje
De pinhole laat maar een zeer smalle lichtbundel door. De diameter van het gaatje bepaalt de grootte van die lichtbundel.
Als deze diameter te klein is, dan zal door diffractie de lichtbundel gespreid worden en krijg je een onscherp beeld.
Anderszijds geeft een te groot gaatje een te brede lichtbundel en ook dit zal dus aanleiding geven tot een onscherp beeld.
De lichtbundel die door het gaatje passeert wordt aan de randen van het gaatje afgebogen en dit maakt dat de beeldcirkel niet scherp afgelijnd is maar aan de randen bijkomende cirkels vertoont. Dit zijn diffractie cirkels.
Hoe kleiner het gaatje hoe meer uitgesproken de diffractiecirkels zijn.

De resolutie
De resolutie of scherpte van het uiteindelijk beeld wordt bepaald door verschillende factoren:
Er is heel wat onderzoek gebeurd naar de optimalisatie van pinholes, vooral door Lord Raleigh (1842-1919).
Zijn formule is de volgende :

DxD = KxLxaxs/(a+s)

waarbij
D = diameter pinhole
L = golflengte van het licht (gemiddeld voor zonlicht = 55 Angstrom of 0,00055 mm)
a = afstand van object tot pinhole
s = afstand van pinhole tot filmvlak
K = een constante


Let op : alle afstanden worden in mm gegeven!!
De constante K is bepalend voor de overlapping van 2 naburige beeldcirkels.
ideaal is de situatie dat K=1 omdat dit de hoogste resolutie oplevert.
Hierbij krijg je dan een zeer grote afstand pinhole-filmvlak, een zeer klein gaatje en dus een zeer donker beeld en extreme belichtingstijden.
Voorbeeld

Je hebt een doos met afstand gaatje-filmvlak = 8 cm.
Je wil een object fotograferen op een afstand van 5 meter.
Welke diameter heeft het gaatje optimaal?

DxD = (K x 0,00055 x 5000 x 80)/(5000 + 80)
Beste resolutie met K = 1 geeft : DxD = 0,0433 en dus D = SQRT(0,0433) = 0,21 mm.
Dit geeft een gaatjescamera met een diafragma-opening f = 80/0,21 = 381

Nemen we een meer praktische K=3 dan wordt de berekening:
DxD = (3 x 0,00055 x 5000 x 80)/(5000 + 80) = 0,1299 en dus D = SQRT(0,1299) = 0,36 mm
De diafragmawaarde is dan f = 222


in de praktijk worden voor K waarden tussen 2 en 3,5 gehanteerd.
voor dichtbij fotografie geeft een kleine K-waarde betere resultaten.

Voor 'normale' fotografie is er deze eenvoudige formule voor het berekenen van de optimale diameter:
D = SQRT(s)/28 *** waarbij s = afstand van pinhole tot filmvlak
Let op : de afstand s in mm geven!!

Hoe maak je een gaatje met een welbepaalde grootte ?
Het gemakkelijkste is om met een injectienaald een gaatje te prikken in een stukje alumiumfolie.
Aangezien de randen van de injectienaald scherp zijn snijden die een cirkeltje uit de alu-folie weg.
Als je met een naald een gaatje prikt dan krijg je een gaatje met flarden van de alu-folie eromheen.
Injectienaalden hebben verschillende diameters, uitgedrukt in Gauge.
Een groter gauge-nummer komt overeen met een kleinere diameter.



Als je een naald gebruikt om een gaatje te prikken heb je hier ook weer nummers.
De standaardmaten voor naalden zijn :



Belangrijk is ook om de f-waarde (het diafragma) te bepalen.

De formule voor berekenen van het diafragma is f=s/D, waarbij f= equivalente f-stop
s= afstand gaatje tot negatief in mm
D= diameter van gaatje in mm

Voorbeeld 1:
We hebben een geschikte zwarte doos met afstand gaatje tot negatief = 15cm (=150mm)
De optimale doormeter van het gaatje D = sqrt(150)/28 = 12,25/28 = 0.44 mm
Voor een s=15 cm en D=0,44mm krijgen we een f=150/0,44= 340

Voorbeeld 2:
We hebben een geschikte metaalfolie met een gaatje van 0,3mm
De optimale afstand gaatje-negatief zal dus gegeven worden als s=(28D)x(28D)= 70,56mm
en dit geeft f=70,56/0,3 = 235


Hoe kunnen we nu de belichtingstijd berekenen?

Nemen we de camera van voorbeeld 2:
meet het licht met een gewone lichtmeter (bv: 1/60 sec voor f:11)
Maar volgens onze berekening heeft onze pinhole camera een f=235
We moeten nu de f-waarde van de meting (f11) verdubbelen tot de f-waarde van de camera bereikt is
11 - 22 - 44 - 88 - 176 - 352


Voor elke verdubbeling van de f-waarde moeten we de belichtingstijd met 4 vermenigvuldigen.
In ons voorbeeld ligt onze f=235 tussen de 176 (= 4 stappen) en 352 (= 5 stappen).
Dit geeft dus tussen de 4x4x4x4 =256 en 4x4x4x4x4 = 1024 maal de gemeten tijd voor f11.

Laten we dus het ongeveer het midden nemen of dus een belichtingstijd = dubbel van de laagste waarde of de helft van de hoogste waarde.
Dit geeft een belichtingstijd = gemeten tijd x 500
Met een gemeten tijd van 1/60 sec wordt de berekende belichtingstijd voor de gaatjescamera : 1/60 x 500 = 8,5 sec.

Maar bij belichtingstijden langer dan 1 seconde moet de effectieve belichtingstijd verlengd worden.
Dit wordt de reciprociteitscorrectiegenoemd.

Een eenvoudige regel is de volgende:

In ons voorbeeld met berekende tijd = 8.5 sec zal de effectieve belichtingstijd dus ongeveer 35 seconden bedragen.

Het is niet nodig om deze berekening te maken telkens als je een foto neemt.
Aangezien een pinhole camera nogal groot is kan je er een tabel op kleven met de gemeten belichtingstijd en de effectieve tijd.

OPGELET : Elke film heeft zijn eigen correctie en dat kan echt wel wat schelen. (zie 5.9.)
Wanneer je bvb. de EFKE 25 (= ADOX 25) zwart-film en de berekende tijd met reciprociteitscorrectie is 10 sec. dan is de belichtingstijds voor een Kodak TMAX 100 film in dezelfde omstandigheden en in dezelfde camera 30 sec.
Voor een Ilford FP4 wordt de effectieve belichtingstijd zelfs 1 minuut.

Het is dus een goed idee om de film waarmee je werkt goed te leren kennen en voor elke film de reciprociteitscorrectie zelf te testen.

In ons voorbeeld geeft dat volgende tabel

De eerste kolom geeft de gemeten tijd met lichtmeter (ingesteld op 100 ASA en f/11).
De tweede kolom geeft de effectieve belichtingstijd voor deze pinhole camera (met f = 235) en voor deze film en rekening houdend met de reciprociteitscorrectie
Zo kun je voor iedere camera met een andere f-waarde en voor elke film een tabel opmaken.


OPMERKINGEN

- Voor een goed resultaat is het belangrijkste onderdeel van een gaatjescamera het gaatje . Dit moet zo perfect mogelijk zijn. Het is niet overdreven om het gaatje onder een microscoop te bekijken op onvolmaaktheden.

- De metaalfolie waarin het gaatje wordt gemaakt moet zo dun mogelijk zijn.
Immers een gaatje in een dikkere folie geeft een soort tunnel-effect wat het eindresultaat slecht beïnvloedt.
De beste gaatjes worden gemaakt door met een laser een gaatje te branden in een flinterdun bronzen plaatje, maar zelf kan je een behoorlijk gaatje produceren door met een injectienaald met een diameter van 0,3mm een gaatje te prikken in aluminiumfolie.

- De grootte van het gaatje is niet echt kritisch. Toch kan je door rekening te houden met de optimale parameters de scherpte van het het eindresultaat veel verbeteren.

- Een gaatjescamera is qua scherpte niet vergelijkbaar met een 'echt' fototoestel. Je hebt altijd een beeld met een soft-focus uitzicht.

- Een interessante eigenschap van de pinhole is dat door de zeer kleine opening (en dus grote f-waarde) er een onvergelijkbare scherptediepte bereikt wordt. Bijna alles is in focus... van zeer dichtbij tot oneindig.




HOOFDSTUK 8: Het zonesysteem